Is There a 40.68-month Cycle?

The Foundation for the Study of Cycles (FSC) has done a lot of work with that cycle over the years.  Some other people contend that more recently the period has averaged 38-39 months. My own analysis of it has convinced me that it is not as important of an agent on stock prices as some people think.

To understand why I come to this conclusion, a bit of background information is helpful.  I come from a mechanical/aerospace engineering background, and so I tend to see things through those eyes.  Cycles in the financial markets can reasonably seen as similar to vibrations of solid bodies that engineers worry about.

Any solid body (and some fluids as well, but that is another matter) will have a natural frequency of vibration, and will also have some degree of damping.  If you take a yard stick and hold one end down on your desk and give it a thwang, you’ll see it vibrate with a natural frequency corresponding to the type and thickness of wood, and to how far you have it extended off the edge of the desk.  Change the length and you’ll change the natural frequency.  And eventually the damping that is inherent to the wood-hand-desk system results in the vibrations diminishing over time, unless you keep thwanging it.

One attribute of natural frequencies is that they also tend to exhibit harmonic oscillations at multiples of the natural frequency.  Thus, the existence of a harmonic oscillation is evidence of a natural frequency being at work.  See this video for a good example of a 2x-harmonic of a twisting oscillation.

Engineers also worry about mechanical systems vibrating or oscillating at the same rate as some excitation frequency.  Your car’s engine is a good example; it rotates and also absorbs oscillating force impulses from the pistons.  No matter how well tuned and balanced it is, you can still feel a little bit of vibration coming through from it at any engine speed.

Ideally, a system should be designed such that the operating RPM of any excitation agent is always different from any of the natural frequencies of system components.  For example, I used to fly OH-58 helicopters (Bell 206) that had a main rotor RPM of 354.  The tailboom was designed with a natural frequency of 172-206, which was just above half the period of the excitation frequency of the main rotor.  Had the tailboom been designed to be stiffer, imparting a higher natural frequency of oscillation, then the designers would have had a lot of problems of tailbooms oscillating wildly and then breaking off (which is a bad thing, trust me).  We had enough problems with vibrations, especially if the main rotor was at all out of balance, and even something as slight as paint erosion on the rotor blades could induce a 1:1 vibration in the helicopter which made flying it a bit like riding a washing machine full of wet towels on spin cycle.

When you see an apparent cycle manifesting itself in the financial markets, the question arises as to whether it is the result of a natural oscillation at some inherent natural frequency, or if instead there is an excitation force occurring at some regular frequency.

Annual seasonality is a great example of an excitation force upon the financial markets.  Some manufacturers have annual production cycles, like autos.  Agriculture is certainly tied to the annual calendar, and its seasonal demands for capital can affect the stock market, which may explain why September and October are often less liquid than other months.  Congress coming back from summer recess also helps to explain ugly Septembers. 
Similarly, the 4-year cycle can be explained as an example of a periodic excitation force that is tied to the US political calendar.  The first two years after a presidential election (starting at Nov. 1) are generally flat, especially during a first term presidency.  The 3rd year is very strong, and the election year is more iffy but generally up.  It is a repeating pattern that I argue is tied to the excitation force of the 4-year election calendar.  The current situation relative to the historical Presidential Cycle Pattern is shown in this chart.  Were we to have a constitutional convention and switch, for example, to Mexico’s 6-year long single-term presidency, we would likely see substantive changes to how the 4-year cycle behaves.

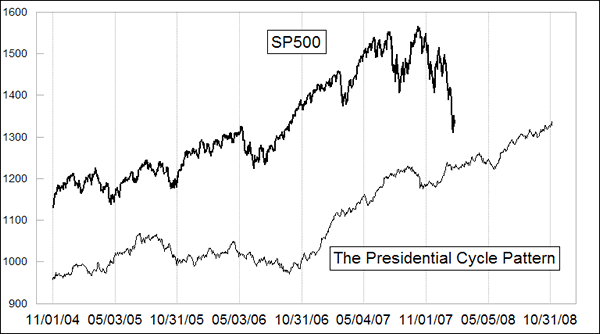
It is tough to argue that the 4-year cycle is the result of a natural frequency, since it does not exhibit the property of harmonics very well.  Any similarities of the first two-year portion of a presidency to the second half are more easily explained as resulting from the effects of annual seasonality.

The 40-week (AKA 9-month) cycle is a great example of a natural frequency in the stock market.  It does exhibit harmonics, with a weaker and slightly more irregular 20-week cycle identifiable as the 1/2-period harmonic.  There is even some evidence of a 10-week cycle, but it is much less regular than the 40-week, which again is typical for a harmonic as opposed to a primary natural frequency.

It is also difficult to explain the existence of the 40-week cycle as being related to some identifiable excitation force.  If it were precisely 9-months long, then we might argue that it was somehow a 3x multiple of the quarterly earnings cycle’s excitation force, but the math does not work out for that to be true.  The earnings cycle hypothesis also does not explain why the 40-week cycle periodically undergoes “phase shift” behavior about every 6-8 years.  Why it is 40 weeks long (or thereabouts) is an interesting question; the only other event that really springs to mind with that same period is human gestation, and it is tough for me to theorize as to why that would matter.

The existence of the 40-week cycle also helps us to understand why the 4-year cycle does not seem to work perfectly, i.e. why does it not bottom every time in October of the 2nd year?  The answer is that 9 months is not evenly divisible into 48 months (4 years), so the 9-month cycle’s arrival time is different from one 4-year cycle period to the next.

All of this lengthy (sorry) lead-up is important to know when contemplating a hypothesis of a 40.68-month cycle that the FSC has promoted quite a bit over the years.  Unless one can tie it to some reasonable excitation force period, then one must therefore infer that it is some sort of natural frequency of the financial markets.  And the best test I know of for that proof is the existence or absence of harmonics behavior.

My own studies of the 40.68-month cycle have shown me that there is not really a good 20-month harmonic, so that is one strike against it.  Another test is for significance, i.e. does a 40.68-month cycle hypothesis pick up the important bottoms one would like to see it predict?  That too has pretty thin evidence.  One could pick some number of months at random and probably find evidence that it “mattered” at some points, sort of like the evidence for Gann Lines, Fibonacci levels, etc.  If you want to find it, you can, but is it really there?

It would be nice if there were a 40-month cycle in the markets.  That would appeal to the senses in terms of a general desire for symmetry, since there are identifiable cycles of 40-weeks and 40(ish)-years, the existence of which has some pretty compelling proof behind them.  But I have looked at it a lot and cannot make the case to myself that it matters more than other factors.